I don’t understand what this has to do with a PhD in cyber security but I do agree with what you said though
- 1 Post
- 121 Comments
Glibc’s qsort will default to either insertion sort mergesort or heapsort. Quicksort itself is used when it cannot allocate extra memory for mergesort or heapsort. Insertion sort is still used in the quicksort code, when there is a final 4 items that need to be sorted.
Normally it is simply mergesort or heapsort. Why I know this? Because there was a recent CVE for quicksort and to reproduce the bug I had to force memory to be unable to be allocated with a max size item. It was interesting reading the source code.
That is if you are not on a recent version of qsort which simply removed quicksort altogether for the mergesort + heapsort
Older version still had quicksort and even some had insertion sort. Its interesting to look at all the different versions of qsort.
I usually ask AI to summarize it and then I get a pretty good idea of what it was meant to do. It’s just another tool to me. AI generated code sucks but it’s nice when it’s a quick summary.
Ah the chaos theory reasoning. There can’t be anything perfect when thinking about it as a whole but you can find sections in a diversified area that are mostly perfect at some point in time but nothing ever lasts.

 2·10 months ago
2·10 months agohaha nice. So the CPython’s
math.sqrtjust hands it off to the C/POSIX implementation of sqrt and even that could possibly be handing it off to the cpu for calculating the square root as fast as possible. my dumb binary search written in complete python is literally matching the speed of some of the most performant methods of doing square root.but you are right, my method of using a binary search isn’t outlandish at all! wow https://stackoverflow.com/questions/3581528/how-is-the-square-root-function-implemented
infact it does seem similar to newton’s method. I just bypassed the entire calculating square root to get the root value and just simply searched for the first single digit integer that will contain the root(ie first and last valid positions)however as the comments to that solution alluded to, when it comes to precision, this method is not worth it. While for us, an approximation that is accurate enough to the single digits is really dam good and might be faster.(while it is not worth to implement for the general sqrt function, unless you know it is needed for extremely low precision tasks or as a challenge)
I sat here thinking I was being dumb for reinventing the wheel lmao

 2·10 months ago
2·10 months agoHonestly as someone who partakes in some cyber security challenges for fun, there are plenty of weird things that programmers or doc writers never ever consider but other times the docs are so barebones that it is worthless to read. And a high word count does not always mean the doc is useful when all the text is either ai generated slop, or a lot of high level ideations that don’t get into how to work it.

 1·10 months ago
1·10 months agoCall it optimization and people will assume it is magic. Instead I call this a simple algebra challenge.(With part two having that quirky concatenation operation)
It is like solving for x. Let’s take an example:
3267: 81 40 27If you change it to equations:
81 (+ or *) 40 (+ or *) 27 = 3267
Which effectively is:
81 (+ or *) 40 = x (+ or *) 27 = 3267So what is the x that either add or multiply would need to create 3267? Or solve for x for only two equations.
x + 27 = 3267->x = 3267 - 27 = 3240
x * 27 = 3267->x = 3267 / 27 = 121(Special note since multiplying and adding will never make a float then a division that will have a remainder(or float) is impossible for x, we can easily remove multiplying as a possible choice)
Now with our example we go plug in x:
81 (+ or *) 40 = (3240 or 121) (+ or *) 27 = 3267So now we see if either 40 or 81 can divide or subtract from x to get the other number. Since it is easier to just program to use the next number in the list, we will use 40.
81 + 40 = 3240->x = 3240 - 40 = 3200 != 81
81 * 40 = 3240->x = 3240 / 40 = 81
81 + 40 = 121->x = 121 - 40 = 81
81 * 40 = 121->x = 121 / 40 = 3.025 != 81This particular example from the website has two solutions.
For the concatenation operation, you simply check if the number ends with the number in the list. If not then a concatenation cannot occur, and if true remove the number from the end and continue in the list.
Call it pruning tree paths but it is simply algebraic.
The goat 🐐
I still like C over Rust. I was thinking of learning Zig for the 2025 aoc
So this means she intentionally let it be seen and possibly wanted something even more rock hard? 😉

 7·11 months ago
7·11 months agoMy phone is starting to take better document pictures than my printer. Especially if I hold my phone steady at the right height. I bet if I used a 3D printer to create a stand to hold it for me. Heck I could buy a giant bucket or rack or whatever and bright high color index lights to further improve image clarity to ungodly levels. Still, the Samsung camera app with the AI features already being preloaded that will likely be improved in the next 5 years will just get better. Printers and scanners are completely a pita.
Oh! I didn’t think it that way, lol, I was thinking this quickly through. I didn’t think of relating to physical locks because it clearly said it was virtual. But I guess, there could theoretically be a physical tumbler lock with 0-5 spacers, it would just be a tall lock. You know like how some master keys have it so that there are spacers for the master key or the client key to open the lock.
Thanks! I quickly wrote it but didn’t think to count things. I just took the index of where the edge was located at and ran with it.
So I don’t understand what you mean by equal 5. Could you elaborate? Cause I must have read the challenge text differently.
Python3
ah well this year ends with a simple ~12.5 ms solve and not too much of a brain teaser. Well at least I got around to solving all of the challenges.
Code
from os.path import dirname,realpath,join from collections.abc import Callable def profiler(method) -> Callable[..., any]: from time import perf_counter_ns def wrapper_method(*args: any, **kwargs: any) -> any: start_time = perf_counter_ns() ret = method(*args, **kwargs) stop_time = perf_counter_ns() - start_time time_len = min(9, ((len(str(stop_time))-1)//3)*3) time_conversion = {9: 'seconds', 6: 'milliseconds', 3: 'microseconds', 0: 'nanoseconds'} print(f"Method {method.__name__} took : {stop_time / (10**time_len)} {time_conversion[time_len]}") return ret return wrapper_method @profiler def solver(locks_and_keys_str: str) -> int: locks_list = [] keys_list = [] for schematic in locks_and_keys_str.split('\n\n'): if schematic[0] == '#': locks_list.append(tuple([column.index('.') for column in zip(*schematic.split())])) else: keys_list.append(tuple([column.index('#') for column in zip(*schematic.split())])) count = 0 for lock_configuration in locks_list: for key_configuration in keys_list: for i,l in enumerate(lock_configuration): if l>key_configuration[i]: # break on the first configuration that is invalid break else: # skipped when loop is broken count += 1 return count if __name__ == "__main__": BASE_DIR = dirname(realpath(__file__)) with open(join(BASE_DIR, r'input'), 'r') as f: input_data = f.read().replace('\r', '').strip() result = solver(input_data) print("Day 25 final solve:", result)

 2·11 months ago
2·11 months agoIt is definitely possible to do it programmatically but like most people including me simply did it manually. though I did do this:
code
# # we step through a proper Ripple Carry adder and check if the gate is correct for the given input. # first level is will start with all the initial input gates. # these must have XOR and AND as gates. marked_problem_gates = defaultdict(lambda: defaultdict(list)) # dict of the full adder as the index and the value of what the next wires lead to. full_adder_dict = defaultdict(lambda: defaultdict(lambda: defaultdict(list))) for i in range(len(wire_states)//2): for (a_key,gate,b_key),output_wire in connections['x'+str(i).rjust(len(next(iter(wire_states)))-1, '0')]: if i == 0: matching_z_wire = 'z' + str(i).rjust(len(next(iter(wire_states)))-1, '0') # we check the first adder as it should have the correct output wire connections for a half adder type. if gate == 'XOR' and output_wire != matching_z_wire: # for the half adder the final sum output bit should be a matching z wire. marked_problem_gates[i][gate].append(((a_key,gate,b_key),output_wire)) elif gate == 'AND' and (output_wire.startswith('z') and (output_wire[1:].isdigit())): # for the half adder the carry over bit should not be a z wire. marked_problem_gates[i][gate].append(((a_key,gate,b_key),output_wire)) if output_wire in connections: full_adder_dict[i][gate][output_wire].extend(connections[output_wire]) else: # since the first adder is a half-adder, we only need to check the other adders to verify that their output wire is not to a z wire. if (output_wire.startswith('z') and (output_wire[1:].isdigit())): # if the output wire is a z wire, we mark the gate as a problem. marked_problem_gates[i][gate].append(((a_key,gate,b_key),output_wire)) else: # we get what the output wires to the next step in the adder would be. full_adder_dict[i][gate][output_wire].extend(connections[output_wire]) # for the next step in the full adders, we expect the carry over bit from the previous step in the adder should be have. # print(marked_problem_gates) print(full_adder_dict)I then took the printed output and cleaned it up a little.
output
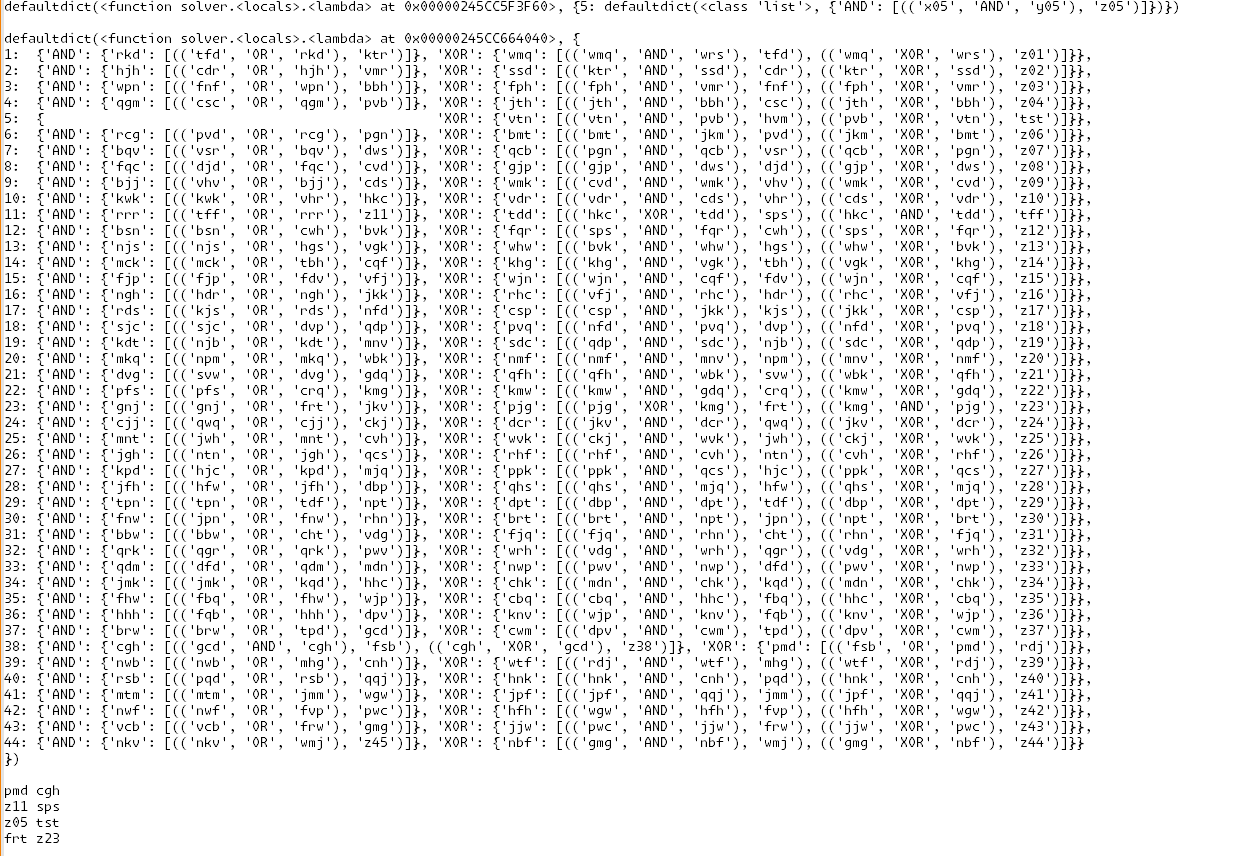
This really just me looking at it and seeing to make sure outputs are connected to the right locations. just took a minute but the highlighting of the selected work helped out. simply faster than just trying to think of some complex logic
basically bruteforce part 2 with our eyes lol
I did notice that most of the swaps where within the fulladders and not accross the entire circuit, so it was a little easier than anticipated.
I only parse each of the initial gates that the input wires to the full adders have
xandyThe only exception is that the first input wires go into a half adder and not a full adder.
So we only verify that theXORgate is connected to an output wirez00and that theANDgate does not output to azwire. EveryANDoutput wire should be connected to one logic gate and that is theORgate for the carry bit.
TheXORgate should have the output wire connected to the two gates that take in the carry bit wire from the previous adder.from there I just used my memory and intuition about full adders to clean up the output and all that to see which of the full adders have bad output wire configs.
Python3
Another day solved with optimized logic
Method build_graph took : 1.554318 milliseconds
Method count_unique_triads took : 943.371 microseconds
Method find_largest_clique took : 933.651 microseconds
Method solver took : 3.800842 millisecondsAgain, Linux handles python better with a final solve time of a combined ~3.8 ms. still it is quite fast on windows with only 0.5 ms increase.
Still having fun adding typing and comments with VSCode + Qwen-coder 1.5B running locally. feels so nice to be proud of readable and optimized code.
Code
from os.path import dirname,realpath,join from itertools import combinations as itertools_combinations from collections import defaultdict from collections.abc import Callable def profiler(method) -> Callable[..., any]: from time import perf_counter_ns def wrapper_method(*args: any, **kwargs: any) -> any: start_time = perf_counter_ns() ret = method(*args, **kwargs) stop_time = perf_counter_ns() - start_time time_len = min(9, ((len(str(stop_time))-1)//3)*3) time_conversion = {9: 'seconds', 6: 'milliseconds', 3: 'microseconds', 0: 'nanoseconds'} print(f"Method {method.__name__} took : {stop_time / (10**time_len)} {time_conversion[time_len]}") return ret return wrapper_method @profiler def build_graph(connections: list[str]) -> defaultdict[set[str]]: """ Builds an adjacency list from the list of connections. """ adj = defaultdict(set) for conn in connections: nodes = conn.strip().split('-') nodes.sort() node1, node2 = nodes adj[node1].add(node2) adj[node2].add(node1) return adj @profiler def count_unique_triads(adj: defaultdict[set[str]]) -> int: """ Counts the number of unique triads where a 't_node' is connected to two other nodes that are also directly connected to each other. Ensures that each triad is counted only once. """ unique_triads = set() # Identify all nodes starting with 't' (case-insensitive) t_nodes = [node for node in adj if node.lower().startswith('t')] for t_node in t_nodes: neighbors = adj[t_node] if len(neighbors) < 2: continue # Need at least two neighbors to form a triad # Generate all unique unordered pairs of neighbors for node1, node2 in itertools_combinations(neighbors, 2): if node2 in adj[node1]: # Create a sorted tuple to represent the triad uniquely triad = tuple(sorted([t_node, node1, node2])) unique_triads.add(triad) return len(unique_triads) def all_connected(nodes: tuple, adj: defaultdict[set[str]]) -> bool: """ Determines if all nodes are connected to each other by checking if every node is reachable from any other node. Effectively determines if a clique exists. """ for i,node in enumerate(nodes): for j in range(i + 1, len(nodes)): if nodes[j] not in adj[node]: return False return True @profiler def find_largest_clique(adj: defaultdict[set[str]]) -> list[str]: """ Iterates over each vertex and its neighbors to find the largest clique. A clique is a subset of nodes where every pair of nodes is connected by an edge. The function returns the vertices of the largest clique found. If no clique is found, it returns an empty list. """ # Keep track of the largest connected set found so far best_connected_set = tuple(['','']) # Iterate over each vertex in the graph with the neighbors for vertex, neighbors in adj.items(): # Since the clique must have all nodes share similar neighbors then we can start with the size of the neighbors and iterate down to a clique size of 2 for i in range(len(neighbors), len(best_connected_set)-1, -1): # we don't check smaller cliques because they will be smaller than the current best connected set if i < len(best_connected_set): break for comb in itertools_combinations(neighbors, r=i): if all_connected(comb, adj): best_connected_set = max( (*comb, vertex), best_connected_set, key=len ) break return sorted(best_connected_set) # Solve Part 1 and Part 2 of the challenge at the same time @profiler def solver(connections: str) -> tuple[int, str]: # Build the graph adj = build_graph(connections.splitlines()) # return the count of unique triads and the largest clique found return count_unique_triads(adj),','.join(find_largest_clique(adj)) if __name__ == "__main__": BASE_DIR = dirname(realpath(__file__)) with open(join(BASE_DIR, r'input'), 'r') as f: input_data = f.read().replace('\r', '').strip() result = solver(input_data) print("Part 1:", result[0], "\nPart 2:", result[1])
I found taking the straight text from the website to GPT o1 can solve it but sometimes GPT o1 produces code that fails to be efficient. so challenges that had scaling on part 2( blinking rocks and lanternfish ) or other ways to cause you to have a hard time creating a fast solution(like the towel one and day 22) are places where they would struggle a lot.
day 12 with the perimeter and all the extra minute details also causes GPT trouble. So does the day 14, especially the easter egg where you need to step through to find it but GPT can’t really solve it because there is not enough context for the tree unless you do some digging on how it should look like.
these were some casual observations. clearly there is more to do to test out, but it shows that these are big struggle points. If we are talking about getting on the leaderboard, then I am glad there are challenges like these in AoC where not relying on an llm is better.
you have a point to call name it something else, but lazy to do that. should I simply call it
solve()maybe, that would work fine.
I do want to note that having it return a value is not unheard of, it is just part of being lazy with the naming of the functions.
I definitely would not have the code outside ofmain()be included in the main function as it is just something to grab the input pass it to the solver function( main in this case, but as you noted should be called something else ) and print out the results. if you imported it as a module, then you can callmain()with any input and get back the results to do whatever you want with. Just something I think makes the code better to look at and use.While doing this is highly unnecessary for these challenge, I wish to keep a little bit of proper syntax than just writing the script with everything at the top level. It feels dirty.
Coding in notepad was a bit brutal, but I stuck with notepad for years and never really cared because I copy pasta quite a bit from documentation or what not.(now a days, gpt helps me fix my shit code, now that hallucinations are reduced decently) even with VSCode, I don’t pay attention to many of its features. I still kinda treat it as a text editor, but extra nagging on top.(nagging is a positive I guess, but I am an ape who gives little fucks) I do like VSCode having a workspace explorer on the side. I dislike needing to alt-tab to various open file explorer windows. Having tabs for open files is really nice, too.
VSCode is nice, and running my Qwen-coder-1.5B locally is neat for helping somethings out. Not like I rely on it for helping with coding, but rather use it for comments or sometimes I stop to think or sometimes the autocomplete is updated in realtime while I am typing. really neat stuff, I think running locally is better than copilot because of it just being more real-time than the latency with interacting with MS servers. though I do think about all the random power it is using and extra waste heat from me constantly typing and it having to constantly keep up with the new context.
The quality took a little hit with the smaller model than just copilot, but so far it is not bad at all for things I expect it to help with. It definitely is capable of helping out. I do get annoyed when the autocomplete tries too hard to help by generating a lot more stuff that I don’t want.(even if the first part of what it generated is what I wanted but the rest is not) thankfully, that is not too often.
I give the local llm is helping with 70% of the comments and 15% of the code on average but it is not too consistent for the code.
For python, there is not enough syntax overhead to worry about and the autocomplete isn’t needed as much.
Python3
Hey there lemmy, I recently transitioned from using notepad to Visual Studio Code along with running a local LLM for autocomplete(faster than copilot, big plus but hot af room)
I was able to make this python script with a bunch of fancy comments and typing silliness. I ended up spamming so many comments. yay documentation! lol
Solve time: ~3 seconds (can swing up to 5 seconds)
Code
from tqdm import tqdm from os.path import dirname,isfile,realpath,join from collections.abc import Callable def profiler(method) -> Callable[..., any]: from time import perf_counter_ns def wrapper_method(*args: any, **kwargs: any) -> any: start_time = perf_counter_ns() ret = method(*args, **kwargs) stop_time = perf_counter_ns() - start_time time_len = min(9, ((len(str(stop_time))-1)//3)*3) time_conversion = {9: 'seconds', 6: 'milliseconds', 3: 'microseconds', 0: 'nanoseconds'} print(f"Method {method.__name__} took : {stop_time / (10**time_len)} {time_conversion[time_len]}") return ret return wrapper_method # Process a secret to a new secret number # @param n: The secret number to be processed # @return: The new secret number after processing def process_secret(n: int) -> int: """ Process a secret number by XORing it with the result of shifting left and right operations on itself. The process involves several bitwise operations to ensure that the resulting number is different from the original one. First, multiply the original secret number by 64 with a left bit shift, then XOR the original secret number with the new number and prune to get a new secret number Second, divide the previous secret number by 32 with a right bit shift, then XOR the previous secret number with the new number and prune to get another new secret number Third, multiply the previous secret number by 2048 with a left bit shift, then XOR the previous secret number with the new number and prune to get the final secret number Finally, return the new secret number after these operations. """ n ^= (n << 6) n &= 0xFFFFFF n ^= (n >> 5) n &= 0xFFFFFF n ^= (n << 11) return n & 0xFFFFFF # Solve Part 1 and Part 2 of the challenge at the same time @profiler def solve(secrets: list[int]) -> tuple[int, int]: # Build a dictionary for each buyer with the tuple of changes being the key and the sum of prices of the earliest occurrence for each buyer as the value # At the same time we solve Part 1 of the challenge by adding the last price for each secret last_price_sum = 0 changes_map = {} for start_secret in (secrets): # Keep track of seen patterns for current secret changes_seen = set() # tuple of last 4 changes # first change is 0 because it is ignored last_four_changes = tuple([ (cur_secret:=process_secret(start_secret)), -(cur_secret%10) + ((cur_secret:=process_secret(cur_secret)) % 10) , -(cur_secret%10) + ((cur_secret:=process_secret(cur_secret)) % 10) , -(cur_secret%10) + ((cur_secret:=process_secret(cur_secret)) % 10) ] ) current_price = sum(last_four_changes) # Map 4-tuple of changes -> sum of prices index of earliest occurrence for all secrets for i in range(3, 1999): # sliding window of last four changes last_four_changes = (*last_four_changes[1:], -(cur_secret%10) + (current_price := (cur_secret:=process_secret(cur_secret)) % 10) ) # if we have seen this pattern before, then we continue to next four changes # otherwise, we add the price to the mapped value # this ensures we only add the first occurence of a patten for each list of prices each secret produces if last_four_changes not in changes_seen: # add to the set of seen patterns for this buyer changes_seen.add(last_four_changes) # If not recorded yet, store the price # i+4 is the index of the price where we sell changes_map[last_four_changes] = changes_map.get(last_four_changes, 0) + current_price # Sum the 2000th price to the total sum for all secrets last_price_sum += cur_secret # Return the sum of all prices at the 2000th iteration and the maximum amount of bananas that one pattern can obtain return last_price_sum,max(changes_map.values()) if __name__ == "__main__": # Read buyers' initial secrets from file or define them here BASE_DIR = dirname(realpath(__file__)) with open(join(BASE_DIR, r'input'), "r") as f: secrets = [int(x) for x in f.read().split()] last_price_sum,best_score = solve(secrets) print("Part 1:") print(f"sum of each of the 2000th secret number:", last_price_sum) print("Part 2:") print("Max bananas for one of patterns:", best_score)
nice job! now do it without recursion. something I always attempt to shy away from as I think it is dirty to do, makes me feel like it is the “lazy man’s” loop.
Aho-Corasick is definitely meant for this kind of challenge that requires finding all occurrences of multiple patterns, something worth reading up on! If you are someone who builds up a util library for future AoC or other projects then that would likely come in to use sometimes.
Another algorithm that is specific to finding one pattern is the Boyer-Moore algorithm. something to mull over: https://softwareengineering.stackexchange.com/a/183757
have to remember we are all discovering new interesting ways to solve similar or same challenges. I am still learning lots, hope to see you around here and next year!


I got two ifixit kits and that’s all I need, even though I stopped repairing the phone and just trade in every three years.